INTRODUCTION
We are living in
an age of information Technology. Electronics is at the very foundation of the
Information and Computer Age. Communications and Computers have made these
tremendous successes that we see today because of the great achievements that
have been recorded in the field of Electronics.
The impact of
electronics have been so deep in almost all areas of our life such as health
care, medical diagnosis and treatment, Air and space travels, Automobiles, etc.
The basis of all the technological innovation and stride made by several
countries of the globe can be directly traceable to their strengths in
electronic design, manufacture, products and services.
We want to
approach the teaching of the knowledge of electronics in the Laboratory Course
by building and testing circuit for practical knowledge of the characteristics
of different devices and in constructing the various circuits. In these Laboratory experience we will
categorize our study of the basic principles of electronics in study about;
(i.) The different components, (ii) Circuits and (iii) measuring instruments
used in electronics.
Components: There are two types of
components that we come across namely Active and Passive components.
Resistors,
capacitors, etc., are known as passive components because they can only
attenuate the electrical voltage and signal and cannot amplify. Whereas devices
like transistors, operational amplifier (Op Amp) can amplify or increase the
amplitude and energy associated with the signals. Hence the transistors and
OpAmp come under active devices.
Circuits: These components can be
combined in different configuration by interconnecting them with conducting
wires to build different electronic modules that provides a predetermined signal type and amplitude given a specific input signal type and amplitude. This module is called an electronic circuits. We would study about
rectifiers, amplifiers, Oscillators, etc., under the category of circuits.
Measuring Instruments: Aside the
components and circuits we must also have familiarity on the principle of
operations and usefulness of some of the essential electronic measuring
instruments such as digital multimeters, regulated power supplies, function
generators, oscilloscopes, etc., These aid trouble shooting of circuits and
identification of faulty components, whenever the circuits that we build do not
work as expected.
PASSIVE ELECTRONICS
COMPONENTS
RESISTORS
Resistors are components that oppose the flow of electrons
(current). The symbols are shown in figure 1.0 below:
Figure 1: Symbols of resistor
Resistance is measured in units called “Ohm” (Symbol; Ω). Multiples
of the units are represented as “kilo-ohms” (kΩ) = 1000 ohms and “mega-ohms” MΩ
= 1000kΩ, that is 106 ohms.
Broadly, we can categorise resistor in to Fixed
Resistors and Variable Resistors.
Fixed Resistors: These
are Carbon Film (5%, 10% tolerance) and
Metal Film Resistors (1%, 2% tolerance) and
wire wound resistors. A fixed
resistor is one for which the value of its resistance is specified and cannot
be varied in general.
Resistance Value
The resistance value is displayed using the color code (the
colored bars/the colored stripes). This is because the average resistor is too
small to have the value printed on it with numbers.
Color Coding:
Color
|
Value
|
Multiplier
|
Tolerance (%)
|
Black
|
0
|
0
|
-
|
Brown
|
1
|
1
|
±1
|
Red
|
2
|
2
|
±2
|
3
|
3
|
±0.05
|
|
Yellow
|
4
|
4
|
-
|
Green
|
5
|
5
|
±0.5
|
Blue
|
6
|
6
|
±0.25
|
Violet
|
7
|
7
|
±0.1
|
Gray
|
8
|
8
|
-
|
White
|
9
|
9
|
-
|
Gold
|
-
|
-1
|
±5
|
Silver
|
-
|
-2
|
±10
|
None
|
-
|
-
|
±20
|
Example 1:
(Red=2), (Green=5), (Orange=3)
Example 2:
(Brown=1), (Black=0), (Orange=3)
10×103 = 10kΩ ohm;
Tolerance (Gold) = ±5%
Example 3:
(Yellow=4), (Violet=7), (Black=0), (Red = 2)
Tolerance: Tolerance
of the resistor is an important property to be considered, a 100Ω resistor with
10% tolerance, means that its value can be any fixed value between 90 to 110
ohms.
Assignment:
Write a short note on the following types of resistors
-
Carbon film resistors
-
Metal film resistors
-
Ceramic resistor
-
Single-in line network resistors
-
Variable resistors
-
Light Dependent Resistance (LDR)
-
Thermistor
Resistor Connections
Individual resistors can be connected together in either a
series connection, a parallel connection or combination of both series and
parallel, to produce more complex resistor network whose equivalent resistance
is the mathematical combination of the individual resistors connected together.
Resistor in Series
Resistors are said to be connected in “Series”, when they are
daisy chained together in a single line. Since all the current flowing through
the first resistor has not other way to go it must also pass through the second
resistor and the third and so on. Then, resistors in series have a Common Current flowing through them as
the current that flows through one resistor must also flow through the others
as it can only take one path.
Then the amount of current that flows through a set of
resistors in series will be the same at all points in a series resistor
network.
For example; in figure 2.1 :
IR1=
IR2= IR3= IAB = 1mA
In the figure 2.1, R1, R2 and R3
are all Connected together in series between points A and B with a common
current, I flowing through them.
Figure 2.1: Resistors in series
As the resistors are connected together in series the same
current passes through each resistor in the chain and the total resistance, RT
of the circuit must be equal to the sum of all the individual resistors added
together. That is;
RT =
R1 +R2 + R3
There for in our example; RT = (1 + 2 + 6)Ω
=
9Ω.
We can see that the circuit in figure 2.1 can be
replaced with figure 2.2 below:
Figure 2.2
REQ in
figure 2.2 is known as equivalent resistance, which can be defined as a single
value of resistance that can replace any number of resistors in series without
altering the values of the current or the voltage in the circuit.
Resistors in Parallel
Resistors are said to be connected together in “Parallel”
when both of their terminals are respectively connected to each terminal of the
other resistor or resistors. Unlike the previous series connection, in a parallel resistor network the circuit
current can take more than one path as there are multiple nodes.
Figure 2.3: Resistors in Parallel
Parallel Resistor Equation:
Then the inverse of the equivalent resistance of two or more
resistors connected in parallel is the algebraic sum of the inverses of the
individual resistance. The equivalent resistance is always less than the
smallest resistor in the parallel network so the total resistance, RT
will always decrease as additional parallel resistors are added.
OHM’S LAW
This is an important and useful law in electronics. It proves
that the current (I) flowing through a conductor is proportional to the voltage
(V) applied across its ends. Mathematically:
V α I or V = IR where R is the
constant of proportionality. R is called Resistance.
Figure 3.0: Useful relationship between Voltage, Current,
Power and Resistance.
Ohm’s Law Circuit
Figure 3.1: Ohm’s Law Circuit
Ideal Voltage Source
Every voltage source (power supply, battery, etc.) has its
own resistance due to its internal construction (this is known as internal resistance). Normally, this
will be generally small of the order of few Ohms only, but it can still be of
significance and cause difficulty in circuits as it will be discussed bellow.
Assume a 6V battery connected to a resistance of (a) 6Ω and
(b) 1Ω. What would be the current according to Ohm’s law?
For (a): I = [6V/6Ω]
= 1A
For (b): I =
[6V/1Ω] = 6A
However, if you actually measured the current you would find
the currents would not be these values.
Figure 3.2: Voltage source showing its internal resistance.
In a typical case, where the internal resistance of the
battery is 1Ω, these currents were 0.86 and 3A only instead of 1A and 6A. Hence
the currents in the two cases are [6V/(6+1)Ω] = 0.86A and [6V/(1+1)Ω]=3A. The voltages
across the internal resistance are 0.86 and 3V and the voltages across the load
resistance are 5.14V and 3V in the two cases respectively.
Ideal Voltage Source
An ideal voltage source is one that has a zero internal
resistance. The process of regulating a power supply, what we really want to do
is reducing its effective internal resistance to as small a value as possible.
In reality, there are not ideal voltage sources, but one can get sources which
are very close to ideal behaviour.
Applying Resistor as Voltage Dividers
Resistors can also be used to
determine voltage, in a configuration called a voltage divider.
Figure 3.3: Voltage divider
The Voltage Division Rule, allows us to use the effects of resistance
proportionality to calculate the potential difference across each resistance
regardless of the current flowing through the series circuit. A typical “voltage
divider circuit” is shown figure 3.3.
The voltage Divider Circuit is the simplest way of producing
a lower voltage from a higher voltage, and is the basic operating mechanism of
the potentiometer.
As well as being used to calculate a lower supply voltage,
the voltage divider formula can also be used in the analysis of more complex
resistive circuits containing both series and parallel branches. The voltage or
potential divide formula can be used to determine the various drops around a
closed DC network or as part of a various circuit analysis laws such as Kirchoffs
of Thevenin’s theorems.
CAPACITORS
A capacitor is basically a device constructed using two parallel
plate separated by an insulator or a dielectric. It is used for storing
electrical energy and capacitor is characterised by very large resistance to
Direct Current (DC) and Smaller resistance for alternating current. It is very
useful as a filter, and for passing AC and blocking DC. The symbol is shown in
figure 4.1 bellow;
Figure 4.1: Symbol
of a capacitor
Figure 4.2: The
Construction of a typical parallel plate capacitor.
The capacitance C of a capacitor is given by;
Where A is the area of the plates, d is the spacing between them,
ε0 is called the permittivity in free space and εr is the
dielectric constant (relative permittivity). With these we can see that the
capacitance of a capacitor is proportional to the area A of the plates and
inversely proportional to the distance between the plates.
When a DC voltage is applied to a capacitor, it gets charged,
just as the charges get accumulated on the plates there is a current flowing in
the circuit. But as the capacitor gets charged the current starts to reduce and
when it is fully charged, the current becomes zero. When we measure the
resistance between the leads of a capacitor it will show infinite resistance,
hence a capacitor will block DC current.
However, when AC voltage or current is applied the
capacitance will offer what we called reactance, it is not resistance, it is
reactance because it is only responding to time varying signals of voltage and
current.
The value of reactance Xc offered by a capacitor is given
by;
The unit of capacitance is Farad (F) , practically, value of
capacitance is very small and thus we use sub-units such as microfarad, μF (10-6F), nanofarad, nF (10-9F),
and picofarad, ρF (10-12F).
Capacitor Connections
Capacitor in Series:
When capacitors are connected in series the resultant
capacitance is much more similar to that of resistors in parallel and is given
by;
or
Figure 4.3: Capacitors in series
Capacitors in
parallel:
When you connect your capacitors in parallel, the total
capacitance can be calculated as you are doing in the case of resistors in
series.
Figure 4.4: Capacitors in Parallel
Breakdown voltage
This is an important characteristic of a capacitor; it is
the maximum voltage that you can apply across a capacitor without breaking down
the capacitor. If you keep on applying voltage to the capacitor, when the
voltage exceeds breakdown voltage,
the dielectric will breakdown making very large current to flow through them. The voltage depends on the kind of
capacitor being used.
Types of Capacitors
Electrolytic Capacitors: The unique
characteristic of this kind of capacitor is that they have polarity i.e. They have positive and a negative electrode.
They range in value from about 1μf to thousands of μf. They a commonly used a
ripple filter in a power supply circuit, or as a filter to bypass
low frequency signals, etc.
Figure 4.5: Electrolytic Capacitors
- Tantalum Capacitors
Tantalum Capacitors are also a type of electrolytic
capacitors that used materials known as tantalum for the electrodes (electrodes are conductors through which
electricity enters or leaves an object, substance, or region). They are
superior to aluminium electrolytic capacitors in temperature and frequency
characteristics, these features make them more expensive.
They a useful in circuit that requires high stability in the
capacitance value, often employed in analogue signal systems.
Figure 4.6: Tantalum
Capacitors
- Ceramic Capacitors
Here they use materials such as titanium and barium oxide as
their dielectric. These type of capacitors are employed in high frequency applications.
Figure 4.7: Ceramic
Capacitors
- Polystyrene Film
Capacitors
As the name obviates, polystyrene film is used as the
dielectric in these devices. They find their applications in filter circuits or
timing circuits with frequency of several hundred KHz or less.
Figure 4.8: Polystyrene film capacitor
This is a “Super Capacitor”, it has a capacitance of 0.47F
(470, 000μF). One should be careful using this type of capacitor in a circuit, because
it has polarity.
Figure: 4.9: Electric double layer capacitors
-Polyester film
capacitors
They use thin polyester film as the dielectric. They are
cheap and handy, having tolerance about ±5% to ±10%.
Figure 4.10: Polyester film capacitors
-
Polypropylene
capacitors
-
Mica Capacitors
-
Dipped mica
capacitors
-
Metallised polyester
film capacitors
-
Variable
capacitors
These capacitors are used in adjusting frequency; here we
can vary the value of capacitance using a special screwdriver.
A coil is a copper wire wound in a spiral.
Figure 4.11: Symbol
of a coil/inductor
The unit of inductance imposed by an inductor is called
Henry (H), the strength of the characteristics of an inductor is directly
proportional to the number of turns it contains. The inductance of a coil can
be greatly increased if it is wound around an iron rod, or ferrite core.
Two importance characteristics of an inductor in a circuit
are:
i.
An inductor can store
energy in its magnetic field and
ii.
It tends to resist any change in the amount of current
flowing through it.
“Lenz’s law illustrated that the direction of induced
current in a coil is such that it opposes the change in the magnetic field that
produced it.
To further illustrate the operation of an inductor see
figure 4.12:
Figure 4.12: Inductor
in a circuit (Source: How Stuff Works 2003).
If the circuit in figure 4.12 is without the inductor, it
normal operation will be that the bulb is ON when the switch is closed and OFF
when the switch is open.
With the inductor L in the circuit, when the switch is
closed, the inductor will want to build up a magnetic field, while
doing this is inhibits the flow of current, this makes the bulb burn brightly
at the onset of closing the key and once the magnetic field has been built the
bulb gets dimmer as current is can now flow normally through the wire.
When the switch is opened after being closed, the magnetic
field in around the coil keeps current flowing in the coil until the filed
collapses. This causes the bulb to burn very brightly for a period of time even
though the switch is open and then quickly goes out. When a current attempts to
change in a conductor, there is a reactance
unlike the case of a capacitor where reactance
is imposed when the voltage attempt to change.
An application of the characteristics of an inductor can be
found in the case of a transformer. In a transformer, the change in current of
one coil affects the current and voltage in the second coil, a phenomenon known
as mutual inductance.
This mutual inductance is also measured in units of the
Henry.
Figure 4.13: Symbol
of a transformer
When AC voltage to the primary coil, due to their mutual
inductance between the primary and secondary coil, there is a voltage also
induced in the secondary and therefore this can be used to get smaller AC
voltage from a larger voltage or a larger voltage from a smaller one.
Relay
Another application of an inductor or coil is in relay. When current flows through a coil
a magnetic filed is produced in a direction of the axis of the coil. The coil
becomes a temporary magnet. In its application in relays this magnet attracts an armature that has been constructed
to make or break an electrical connection due to the attraction. When the
current to the coil is switched off, the armature is returned by a force,
approximately half as strong as magnetic force, usually produced by a spring,
to its relaxed position.
Figure 4.14: Image
of a typical Relay
Resonance
Inductors and Capacitors combined in a circuit (tank
circuit) produce a special characteristic. The impedance (i.e. resistance to
the flow of current) of the circuit changes with the frequency of the voltage. This
characteristic is employed in tuning circuit that select a particular radio
station.


















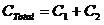











No comments:
Post a Comment
Please drop your comment here, thanks.